Was 1,8 % ausmachen
In diesem Beispiel möchte ich untersuchen, wie sich unterschiedlich hohe Gebühren auf die Performance auswirken.
Dazu vergleiche ich zwei Aktienfonds miteinander. Beide sollen weltweit in große Standardwerte investieren. Beide Fonds sollen jedes Jahr 3 % an Rendite bringen. Der einzige Unterschied zwischen den beiden:
- Fonds 1 verlangt 0,2 % Gebühren
- Fonds 2 verlangt 2 % Gebühren
Was wird aus 10.000 Euro?
Wir stecken heute einmalig 10.000 Euro in beide Fonds und starten dann die Excel-Simulation.
Wie werden sich unsere 10.000 Euro über die nächsten 30 Jahre entwickeln? Die Tabelle zeigt es.
Zum Thema 30 Jahre: So lange ist das nicht. Wer mit 30 Jahren 10.000 Euro anlegt, verfügt mit 60 über das Geld. Wer erst mit 40 beginnt, ist 70, wenn die Auszahlung fällig wird. Das ist zwar schon alt, aber noch kein Zeitpunkt zum Sterben. Ich finde, dass 30 Jahre ein sehr realistischer Anlagezeitraum sind.
| Zeitraum in Jahren |
0,2 % Kosten |
2 % Kosten |
Delta |
Delta in % |
| 1 |
10.279,40 € |
10.094,00 € |
185,40 € |
1,8 % |
| 5 |
11.477,28 € |
10.478,92 € |
998,36 € |
9,5 % |
| 10 |
13.172,79 € |
10.980,78 € |
2.192,01 € |
20,0 % |
| 15 |
15.118,77 € |
11.506,67 € |
3.612,10 € |
31,4 % |
| 20 |
17.352,23 € |
12.057,74 € |
5.294,49 € |
43,9 % |
| 25 |
19.915,63€ |
12.635,21 € |
7.280,42 € |
57,6 % |
| 30 |
22.857,72 € |
13.240,34 € |
9.617,38 € |
72,6 % |
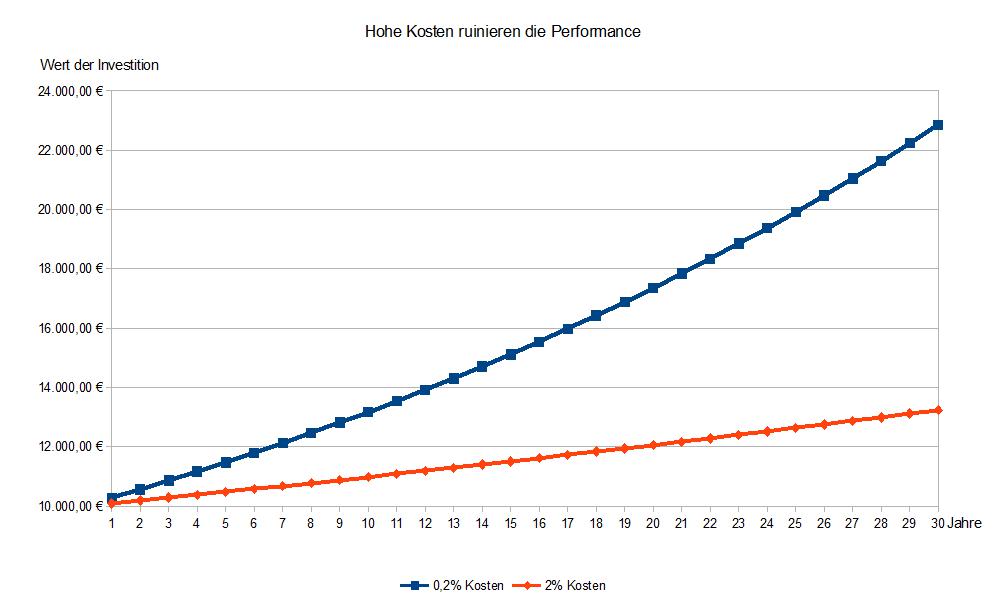
Nach 30 Jahren hat sich eine Kostendifferenz von 1,8 % in einen satten Vorsprung von 72,6 % verwandelt. Absolut gesehen hat Fonds 1 knapp 10.000 Euro mehr gebracht. Allein durch die Kraft des Zinseszinses hat sich das Geld in Fonds 1 mehr als verdoppelt, während Fonds 2 gerade mal gut 3.000 Euro bringt.
In meinen Augen ein ziemlich mickriger Ertrag für eine Wartezeit von 30 Jahren.
Wie wirkt sich der Ausgabeaufschlag aus?
Die Hardcore-Variante:
- Fonds 1 verlangt 0,2 % Gebühren
- Fonds 2 verlangt 2 % Gebühren und nimmt 5 % Ausgabeaufschlag.
Ausgabeaufschlag? Das ist so eine Art Türstehergebühr. Der Fonds verlangt 5 % der Anlagesumme einfach dafür, dass Sie mitmachen dürfen. "Du willst uns 10.000 Euro geben? Na gut. Aber nur, wenn du uns das mit 500 Euro versüßt." Für Sie bedeutet das: Sie gehen im Jahr 1 mit 9.500 € ins Rennen.
- Fonds 1 bringt 3 % von 10.000 € und zwackt davon 0,2 % ab.
- Fonds 2 bringt 3 % von 9.500 € und zwackt davon 2 % ab.
Letztendlich bedeutet das für Sie: Sie müssen 6 (in Worten sechs) Jahre warten, bis Sie endlich wieder die Nulllinie überqueren. Sie erinnern sich: Sie hatten 10.000 Euro abgeliefert ‒ erst im Jahre 6 nach der Einzahlung überspringt Ihr Fondsanteil wieder die 10.000-Euro-Grenze.
Nach 30 Jahren haben Sie ein Plus von knapp 2.600 Euro erwirtschaftet, während Fonds 1 mit einem Gewinn von knapp 13.000 Euro vom Platz geht.
| Zeitraum in Jahren |
0,2 % Kosten |
2 % Kosten + 5 % AA |
Delta |
Delta in % |
| 1 |
10.279,40 € |
9.589,30 € |
690,10 € |
7,2 % |
| 5 |
11.477,28 € |
9.954,97 € |
1522,30 € |
15,3 % |
| 10 |
13.172,79 € |
10.431,74 € |
2.741,05 € |
26,3 % |
| 15 |
15.118,77 € |
10.931,33 € |
4.187,44 € |
38,3 % |
| 20 |
17.352,23 € |
11.454,86 € |
5.897,38 € |
51,5 % |
| 25 |
19.915,63€ |
12.003,45 € |
7.912,18 € |
65,9 % |
| 30 |
22.857,72 € |
12.578,32 € |
10.279,40 € |
81,7 % |
Diese Grafik zeigt das ganze Elend.
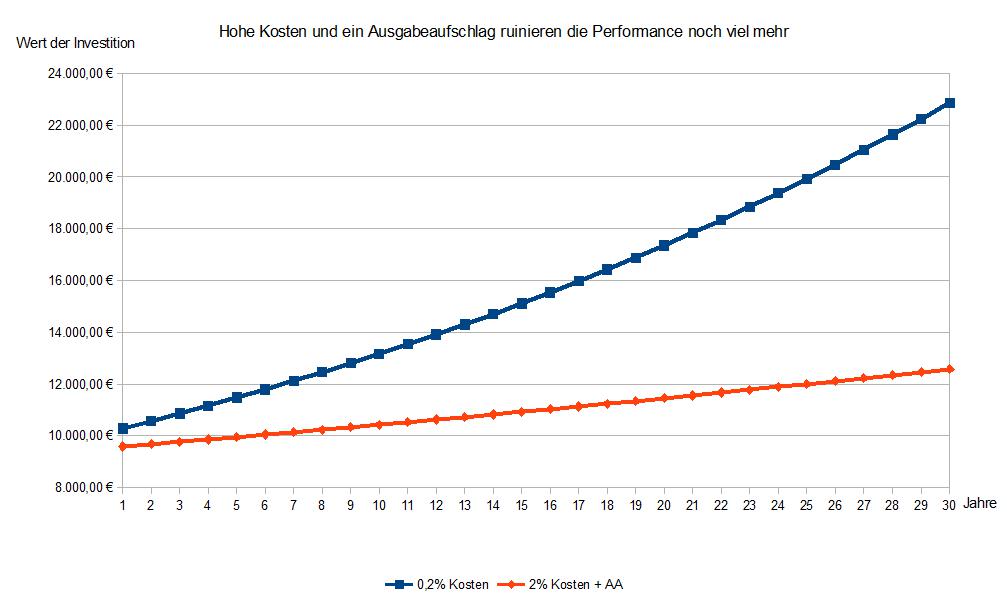
Der Ausgabeaufschlag ruiniert alles
Der anfängliche Verlust der 500 Euro durch den Ausgabeaufschlag ist nie mehr aufzuholen. Die Kombi hohe Gebühren + Ausgabeaufschlag bricht jeder Investition das Genick. Der Fonds hat ja nicht schlecht performt, aber die Gebühren haben ihm das Fleisch von den Knochen genagt.
Der Ausgabeaufschlag wirkt sich deshalb so verheerend aus, weil er ganz am Anfang abgezogen wird.
Wenn Sie einen Euro heute zu 3 % anlegen, dann bekommen Sie nach einem Jahr den Euro zurück und dazu 3 Cent Zinsen. Wenn Sie den Euro nicht anlegen, sondern sich ein Eis dafür kaufen, dann verzichten Sie aufs Jahr gesehen auf 3 Cent Zinsen. Dieser Verlust ist zu verschmerzen.
Wenn Sie heute einen Euro zu 3 % anlegen und 30 Jahre warten, dann bekommen Sie nach 30 Jahren den Euro zurück und 1,36 Euro an Zinsen. Das Faszinierende dabei: Sie bekommen nach 30 Jahren nicht bloß das 30fache des Einjahreszinses, sondern mehr als das 45fache des Einjahreszinses (1,36 € /0,03 €).
Wenn man die Endstände der beiden Varianten mit/ohne Ausgabeaufschlag vergleicht, stellt man fest, dass der Abstand der beiden Fonds nicht geringer wird, sondern größer.
| Zeitpunkt |
Fonds 2 % ohne AA |
Fonds 2 % mit AA |
Delta |
| Start |
10.000,00 € |
9.500,00 € |
500,00 € |
| Ende |
13.240,34 € |
12.578,32 € |
662,02 € |
(awa)
Der Freitags-Newsletter
Hat Ihnen dieser Artikel gefallen? Wollen Sie wisssen, wenn sich hier etwas tut (unter anderem neue Artikel, Veranstaltungen mit und von mir)? Wenn ja, dann melden Sie sich zum Freitags-Newsletter an.
Ja, ich bin dabei!
kurz & bündig, kostenlos, kein Spam, keine Weitergabe der E-Mail-Adresse, jederzeit kündbar, Datenschutz
Abgelegt unter Geldanlage, Grundlagen, Zinsen, Rendite
Das könnte Sie auch interessieren
- Einer ist gut, zwei wären besser, am besten wären drei
- Sind Sie der Friedrich Merz von nebenan?
- Diese 4 Bio-Strategien sollten Sie kennen
- Leserfrage: Ist der MSCI World Small Cap ein guter Einsteiger-ETF?
Kommentare
Bjoern sagt am 12. Februar 2016
Toller Artikel, der im Prinzip ja auch stimmt.
Nur sollte man in die Berechnung einfließen lassen, dass viele v.a. teure Fonds sich ja damit schmücken, den Index zu schlagen. Ich weiß, 90% schlagen den Index nicht.
Aber mal angenommen, DER Top-Fonds schlägt den Index um 1-2% - wie würde sich das ganze dann auswirken? Klar, mit 2% mehr Kosten und 5% Ausgabeaufschlag hinkt dieser immernoch dem ETF hinterher; aber zumindest wohl nicht mehr so krass wie im unteren Beispiel, wo du für den Top-Fonds sowie für den ETF gleiche Rendite angenommen hattest :-)
Phoenix sagt am 12. Februar 2016
@Bjoern:
Aber das ist ja genau das Problem! Niemand kennt den "Top-Fonds" von morgen. Mach dir doch einfach mal den Spaß und suche nach Artikeln, die vor 1, 5 und 10 Jahren veröffentlicht worden sind und schau nach, welche Fonds da als "die absolut sicheren Top-Performer" verkauft werden.Und dann vergleich das mal im Nachhinein mit ihrer echten Performance.
Wenn du mit Sicherheit und garantiert sagen kannst, welcher Fonds seinen Index schlagen wird, dann sag Bescheid. Ich investiere dann sofort alle meine Mittel darein ;)
Matheschwänzer sagt am 15. April 2019
Auch wenn der Artikel nun einige Jahre alt ist, aber die Zahlen verstehe ich nicht ganz.
Für das erste Jahr sind folgende Werte gegeben:
1 10.279,40 € 10.094,00 € 185,40 € 1,8 %
2,8% von 10.000 € wären für mich 280 €, und 1% von 10.000 € ziemlich genau 100 €.
Woraus ergibt sich die Differenz von 60 Cent resp. 6 € in den angegebenen Werten für das erste Jahr?
ChrisS sagt am 15. April 2019
@ Matheschwänzer
der Wesir hat wahrscheinlich so gerechnet, die Kosten zuerst abzuziehen, und erst hinterher die Rendite drauf.
Bsp:
Bei der Frage, welche Variante nun die (mathematisch) ganz korrekte ist - also ob zuerst Kosten ab, dann Rendite drauf, oder auch zuerst Rendite drauf und danach erst Kosten weg gerechnet werden darf/muss, oder ob der Einfachheit halber beides sogar gleichzeitig miteinander verrechnet werden kann (ala 3 - 0,2 = 2,8 %) kann man sich nun drüber streiten wenn man will, je nachdem mit welchen Modellannahmen über das zugrundeliegende Produktverhalten gemacht werden (zB. ob die Kosten eben komplett am Anfang eines Jahres, am Ende eines Jahres, oder stetig fortlaufend anteilig abgezogen werden).
Matthias sagt am 15. April 2019
Hallo Matheschwänzer,
der Wesir hat erst die Jahresrendite von 3% zur Investitionssumme addiert.
Also: 10.000 Euro + 300 Euro ergibt 10.300 Euro.
Und von diesem Wert hat er dann die Kosten in Höhe von 0,2% bzw. 2% abgezogen.
- 0,2% von 10.300 Euro sind 20,60 Euro, abgezogen von 10.300 Euro ergibt 10.279,40 Euro.
- 2% von 10.300 Euro sind 206 Euro, abgezogen von 10.300 Euro ergibt 10.094 Euro.
Viele Grüße
Timo sagt am 15. April 2019
Hallo Matheschwänzer,
die Rechnung ist so aufgestellt, dass die Kosten am Ende des Jahres abgezogen werden. Also zuerst kommt die Rendite (10.000€ 1,03 = 10.300€), DANACH werden die Kosten abgezogen. Also
10.300€ 0,998 = 10.279,40€ bzw. 10.300€ * 0,98 = 10.094€
ich habe das nur für die Zeile durchgerechnet, aber ich vermute, dass setzt sich so fort.
Dummerchen sagt am 16. April 2019
@Matheschwänzer:
Albert hat die Kosten auf die Gesamtsumme (also nach Gewinn) berechnet:
- 10.000€*103%=10.300€
- 10.300€*99.8%=10279,4€
- 10.300€*98%=10094€
Liebe Grüße
Dummerchen
ChrisS sagt am 17. April 2019
Natürlich fällt mir erst hinterher wieder ein dass man Multiplikationen an beliebiger Stelle verketten kann und es daher keine Rolle spielt ob zuerst die Rendite drauf-, und die Kosten abgezogen werden, oder andersrum, beides führt am Ende zum gleichen Ergebnis. :-D
Bleibt noch am Ende die eher akademische Frage ob dies aber (Rendite und Kosten getrennt voneinander auf einen Schlag ansetzen) die passende ist, oder ob nicht auch die einfache "Verrechnungsmethode" (wie im Beispiel: 3% - 0,2% = 2,8%) für Investmentprodukte wie ETFs/Fonds besser (realistischer) ist, da sie ja fortlaufend kontinuierlich "verzinst" werden (sich prozentual weiterentwickeln) - ja, natürlich nicht so konstant wie in den vereinfachten Beispielrechnungen, sondern in der Realität natürlich täglich schwankend - und auch die Kosten genauso nicht nur an einem einzigen Stichtag (egal ob der nun am Anfang oder Ende liegt) komplett entnommen werden, sondern mehr oder weniger auch genauso kontinuierlich anteilig in vielen kleinen Schritten.
Grad mal den Fonds-Rechner auf https://www.zinsen-berechnen.de/fondsrechner.php bemüht, um zu sehen ob/was das für einen Unterschied langfristig machen würde.
Gleiche Ausgangslage: 10.000€ über 30 Jahre lang investiert (keine weitere monatl. Sparrate etc.) in eine Anlage mit 3 % Rendite, einmal mit 0,2 % Verwaltungsgebühren und einmal mit 2%.
Fall A
0,2 % Gebühren, getrennt von der Rendite 3% (wie Finanzwesir-Artikel etc.), ergibt nach 30 J
22.862,36 € Endwert, bzw effektive Rendite 2,795 % pa
"Verrechnung", also (3% - 0,2% =) 2,8 % Rendite (und dazu "keine" Gebühren noch extra eingegeben) ergibt nach 30 J
22.897,78 € Endwert, bzw eben die effektive Rendite von 2,8 % pa
Fall B
2 % Gebühren, getrennt von 3% Rendite, ergibt nach 30 J
13.334,13 € Endwert, bzw effektive Rendite von 0,964 % pa
"Verrechnung", also (3 - 2 =) 1% effektive Rendite nach Gebühren, ergibt nach 30 J
13.478,49 € Endwert, bzw effektive Rendite von eben 1 % pa
Dass beides nicht identisch ist, haben wir ja schon vorher gewußt (von daher kann man sich gern an eine der Methoden halten, die man für die korrekte hält), aber die Unterschiede sind jetzt auch nicht in der Größenordnung dass sie zu völlig divergenten Schlüssen kommen oder eine Methode davon völlig unbrauchbar ist.
Marius sagt am 22. April 2019
Ein Ausgabeaufschlag von 5% reduziert das Startkapital aber nicht um 5%, sonst würde er ja Ausgabeabschlag heißen.
Also korrekt wäre 10.000 Euro * (1/1,05)= 9.523,81 Euro.
Den Ausgabeaufschlag bekommt auch nicht der Fonds wir der Finanzwesir schreibt sondern die Bank als Vermittlungsprovision.
Finanzwesir sagt am 23. April 2019
Hallo Marius,
"Ein Ausgabeaufschlag von 5% reduziert das Startkapital aber nicht um 5%, sonst würde er ja Ausgabeabschlag heißen."
Du liegst teilrichtig ;-) Aber hier geht es nicht nach Mathematik und gesundem Menschenverstand, sondern nach Profitmaximierung.
Das was Du vorschlägst nennt sich Nettomethode und ist eine Art den AA zu berechen. Es gibt aber auch Fondsanbieter, die den Aufschlag auf den höheren Ausgabepreis berechnen. Das ist die Bruttomethode.
Wenn der Ausgabeaufschlag nur in Prozent angegeben wird ist nicht klar, welche Berechnungsmethode der Fonds ansetzt.
Dann gilt: In dubio pro Anleger und ich rechne mit der anlegerschädlichsten Variante.
Gruß
Finanzwesir
IsaRos sagt am 10. Juli 2020
Was leider nicht herausgearbeitet wurde:
0% Ausgabeaufschlag und 5% AA machen bei der Variante 2% Jahresgebühr ein Delta von 600€ aus. Vergleicht man 0,2% JG mal ohne und mal mit 5% AA ist das Della 1.100€. Der reine Unterschied zwischen 0,2% und 2% JG jeweils ohne AA sind aber 9.400€! Jeweils mit 5% AA sind es 8.900€. Ein AA selbst von 5% ist somit tatsächlich fast irrelevant, wenn man mit JG um die 2% zu tun hat.
Darum macht das zwangshafte optimieren der einmaligen Transaktionsgebühren (denn nichts anderes ist ein AA) keinen Sinn, wenn man dafür schlechtere JG (= eine höhere TER) in Kauf nehmen muss, z.B. weil es bei TradeRepublik keine Vanguard Fonds gibt, sondern nur iShares.



